Ableitung: Produktregel (Analysis)

1. Einleitung

Die Produktregel dient dazu, ein Produkt aus zwei oder mehr Funktionen einfacher abzuleiten. Zum Beispiel:

oder auch

Meistens könnte man die Anwendung der Produktregel zwar vermeiden, indem man einfach ausmultipliziert - mit der Produktregel geht es aber auf Dauer einfacher.

2. Die Regel

Die Produktregel definiert sich folgendermaßen:
Will man eine Funktion ableiten, die durch

gegeben ist, dann ist die Ableitung dieser Funktion

Die Produktregel ändert sich nicht wesentlich, wenn man mehr als zwei Faktoren zum Ableiten hat. Zwar bekommt man zumeist auch nur zwei Faktoren zum Ableiten in der Schule vorgelegt, es ist aber trotzdem interessant sich das ganze für mehr anzuschauen, denn erst dann kann man die "Gleichmäßigkeit" der Produktregel erkennen (und sie sich leichter merken!).
Wir schreiben nun statt "u(x)" einfach "u", statt "u ' (x)" "u' " und entsprechendes für die anderen Faktoren.

Na, die gut versteckte Regelmäßigkeit erkannt? ;) Nun sollte es auch leichter sein, sich die Grundform zu merken.

3. Beispiel 1

Ein einfaches erstes Beispiel
(das würde man wohl normalerweise einfach ausmultiplizieren):

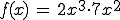
Nun schreibt man sich eine kleine Übersicht auf,
dann muss man nicht alles im Kopf rechnen
(zumindest am Anfang nützlich):

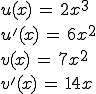
u(x)=2x^3, u'(x)=6x, v(x)=7x^2, v'(x)=14x

Nun noch einmal die Formel, dann einsetzen und ausrechnen:

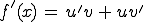
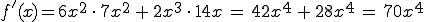
f'(x)=6x^2*7x^2+2x^3*14x=42x^4+28x^4=70x^4

Und damit ist die Ableitung errechnet!

4. Beispiel 2

Nun einmal eine schwierigere Funktion:

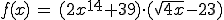
$f(x)=(2x^{14}+39)(wurzel(4x)-23)$

Wieder die Übersicht über u, u', v und v':

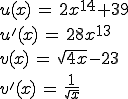
$u(x)=2x^{14}+39, u'(x)=28x^{13}, v(x)=wurzel(4x)-23, v'(x)=1/wurzel(2x)$

Und nun das ganze wieder einsetzen und ausrechnen:

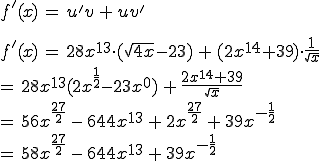
f'(x)=58x^(27/2)-644x^13+39x^(-1/2)

Kommentare (31)

Von neu nach alt

Das Erstellen neuer Kommentare ist aufgrund der Einführung der europäischen Datenschutz-Grundverordnung (DSGVO) derzeit deaktiviert.
Wir bitten um ihr Verständnis.

1/wurzel 2x ist auch richtig ;)

wir kommen als ableitung auf 1/wurzel 2x

wie kommt´s du auf 1/wurzel x als Ableitung von wurzel 4x minus 23 ?

Danke^^

von meinem Freund: biste auf droge oder was ?^^ :)

Hallo

@ArnoNuehm denke auch bin auf die selbe ableitung wie du gekommen da du ja 2x^-0,5 via Potenz bzw. Wurzelgesetze wieder zweimal umschreiben kannst also zu 1/2x^0,5 und ann zu 1/Wurzel aus 2x

Da hat sich wohl der Fehlerteufel eingeschlichen. ich komme als Lösung auf :

(58*x^14-644*x^(27/2)+39)/sqrt(x)

sqrt(x) bedeutet wurzel(x)

müsste die ableitung von {4x} nicht 1/{2x} sein da:

{4x} = (4x)^1/2 , dann Ableitung: 2x^-1/2 , daraus folgt --> 1/(2x^1/2) und das ist 1/{2x}:D

müsste die ableitung von {4x} nicht 1/2x sein da:

{4x} = (4x)^1/2 , dann Ableitung: 2x^-1/2 , daraus folgt --> 1/(2x^1/2) und das ist 1/{2x}:D

Super, vielen Dank^^

Echt gut erklärt, dass hab ich gebraucht.

@ ArnoNuehm

u(x)= 1/x = x^(-1) => u'(x)=-x^(-2)

Diese Klammer "{}" ist mein Zeichen für Wurzel

v(x)= {x} = x^(1/2) => v'(x)=1/2*x^(-1/2)

also:

f'(x)= -x^(-2)*x^(1/2) + 1/x * 1/2*x^(-1/2)

Ausrechen musst du selber ;-)

Alle Kommentare zeigen (31)

Ableitung: Produktregel (Thema: Analysis)

Das richtige Ableiten von Produkten in der Differentialrechnung